Оператори та вирази

Оператори та вирази#

uk-flagанглійська: Operators and Expressions

Більшість statements (логічних рядків), які ви пишете, міститимуть вирази. Простим прикладом виразу є 2 + 3. Вираз можна розбити на оператори та операнди.

Оператори — це певний функціонал, який виконує певні дії та який може бути представлений такими символами, як наприклад «+», або спеціальними ключовими словами. Операторам потрібні деякі дані для роботи, і такі дані називаються операндами. У цьому випадку “2” і “3” є операндами.

Оператори#

uk-flagанглійська: Operators

Ми коротко розглянемо оператори та їх використання.

Зверніть увагу, що ви можете обчислити вирази, наведені у прикладах, використовуючи інтерпретатор інтерактивно. Наприклад, щоб перевірити вираз 2 + 3, скористайтесь інтерактивним командним рядком інтерпретатора Python:

код Python (використовуючи idle)

>>>2 + 3
5
>>>3 * 5
15
>>>

Ось короткий огляд доступних операторів:

  • + (Плюс, uk-flagанглійська: plus)

    • Підсумовує два об’єкта

    • 3 + 5 дорівнює 8. 'a' + 'b' дорівнює 'ab'.

  • - (Мінус, uk-flagанглійська: minus)

    • Дає віднімання одного числа від іншого; якщо перший операнд відсутній, він вважається нульовим.

    • -5.2 дасть негативне число, а 50 - 24 дасть 26.

  • * (Mноження, uk-flagанглійська: multiply)

    • Видає множення двох чисел або повертає рядок, що повторюється задане число разів.

    • 2 * 3 дорівнює 6. 'la' * 3 дорівнює 'lalala'.

  • ** (Піднесення до степеня, uk-flagанглійська: power)

    • Повертає число х, зведене в ступінь y

    • 3 ** 4 дорівнює 81 (тобто 3 * 3 * 3 * 3)

  • / (Ділення, uk-flagанглійська: divide)

    • Ділить x на y

    • 13 / 3 дорівнює 4.333333333333333

  • // (Цілочисельний поділ, uk-flagанглійська: divide and floor)

    • Розділіть x на y та округліть відповідь вниз до найближчого цілого значення. Зауважте, що якщо одне зі значень є числом з плаваючою комою, ви отримаєте значення з плаваючою комою.

    • 13 // 3 дорівнює 4

    • -13 // 3 дорівнює -5

    • 9//1.81 дорівнює 4.0

  • % (Поділ по модулю, uk-flagанглійська: modulo)

    • Повертає залишок від ділення

    • 13 % 3 дорівнює 1. -25.5 % 2.25 дорівнює 1.5.

  • << (Оператори зсуву вліво на задану кількість біт, uk-flagанглійська: left shift)

    • Зсуває біти числа вліво на задане число позицій. (Кожне число представлено в пам’яті бітами або двійковими цифрами, тобто 0 і 1)

    • 2 << 2 дорівнює 8. У двійковій системи числення 2 представляє собою10.

    • Зрушення вліво на 2 біта дає «1000», що у десятковій системи числення означає 8.

  • >> (Оператори зсуву вправо на задану кількість біт, uk-flagанглійська: right shift)

    • Зсуває біти числа вправо на задане число позицій.

    • 11 >> 1 дорівнює 5.

    • У двійковій системи числення 11 представлено в бітах як 1011 яке при зсуві вправо на 1 біт дорівнює 101 і яке є десятковим 5.

  • & (Побітове І, uk-flagанглійська: bit-wise AND)

    • Побітова операція І над числами: якщо обидва біти дорівнюють 1, то результат дорівнює 1. В іншому випадку це 0.

    • 5 & 3 дорівнює 1 (0101 & 0011 дорівнює 0001)

  • | (Побітове АБО, uk-flagанглійська: bit-wise OR)

    • Побітова операція АБО над числами: якщо обидва біти дорівнюють 0, результат 0. В іншому випадку це 1.

    • 5 | 3 дорівнює 7 (0101 | 0011 дорівнює 0111)

  • ^ (Побітове виключне АБО, uk-flagанглійська: bit-wise XOR)

    • Побітова операція виключне АБО над числами: якщо обидва біти (1 або 0) однакові, результат дорівнює 0. В іншому випадку це 1.

    • 5 ^ 3 дорівнює 6 (O101 ^ 0011 дорівнює 0110)

  • ~(Побітове НЕ, uk-flagанглійська: bit-wise invert)

    • Побітова операція НЕ для числа x відповідає -(x+1)

    • ~5 дорівнює -6. Детальніше на http://stackoverflow.com/a/11810203

  • < (Менше ніж, uk-flagанглійська: less than)

    • Визначає чи вірно те, що x менше за y. Усі оператори порівняння повертаютьTrue або False. Зверніть увагу на написання цих імен з великої літери.

    • 5 < 3 дорівнює False, а 3 < 5 дорівнює True.

    • Можна складати довільні ланцюжки: 3 < 5 < 7 дає True.

  • > (Більше ніж, uk-flagанглійська: greater than)

    • Визначає чи вірно те, що x більше за y

    • 5 > 3 повертає True. Якщо обидва операнди є числами, вони спочатку перетворюються на однаковий тип. В іншому випадку завжди повертається False.

  • <= (менше або дорівнює, uk-flagанглійська: less than or equal to)

    • Визначає чи вірно те, що x менше або дорівнює y

    • x = 3; y = 6; x <= y повертає True

  • >= (більше або дорівнює, англ.» uk-flagанглійська: greater than or equal to)

    • Визначає чи вірно те, що x більше або дорівнює y

    • x = 4; y = 3; x >= 3 повертає True

  • == (дорівнює, uk-flagанглійська: equal to)

    • Порівнює, чи однакові об’єкти

    • x = 2; y = 2; x == y повертаєTrue

    • x = 'str'; y = 'stR'; x == y повертає False

    • x = 'str'; y = 'str'; x == y повертає True

  • != (не дорівнює, uk-flagанглійська: not equal to)

    • Порівнює, якщо об’єкти не рівні

    • x = 2; y = 3; x != y повертає True

  • not (логічне НЕ, uk-flagанглійська: boolean NOT)

    • Якщо x дорівнює True, оператор поверне False. Якщо ж x дорівнює False, отримаємо True.

    • x = True; not x повертає False.

  • and (логічне І, uk-flagанглійська: boolean AND)

    • x and y повертає False,якщо x дорівнює False,в протилежному випадку(х=True) повертає значення y

    • x = False; y = True; x and y повертає False оскільки x є False. У цьому випадку Python не обчислюватиме y, оскільки він знає, що ліва частина виразу «and» має значення «False», що означає, що весь вираз буде «False» незалежно від інших значень. Це називається скороченою оцінкою булевих (логічних) виразів (англ. “short-circuit evaluation”).

  • or (логічне АБО, uk-flagанглійська: boolean OR)

    • Якщо x дорівнює True, він повертає True, в протилежному випадку отримаємо значення y

    • x = True; y = False; x or y повертає True.Тут також застосовується скорочена оцінка виразів.

Короткий запис математичних операцій та привласнення#

Зазвичай виконується математична операція над змінною, а потім привласнюється результат цієї операції тій самій змінній, отже, для таких виразів існує скорочення:

a = 2
a = a * 3

можна записати як:

a = 2
a *= 3

Зверніть увагу, що вирази виду var = var operation expression(“змінна = змінна операція вираз”) стає var operation= expression(“змінна операція = вираз”).

Порядок обчислення#

uk-flagанглійська: evaluation Order

Якщо у вас є такий вираз, як «2 + 3 * 4», спочатку виконується додавання чи множення? Шкільний курс математики говорить нам, що спочатку потрібно виконати множення. Це означає, що оператор множення має вищий пріоритет, ніж оператор додавання.

У наcтупній таблиці нижче наведено пріоритет операторів Python, починаючи з самого найнижчого пріоритету (найслабше зв’язування, англ.“least binding”) до найвищого пріоритету (найсильніше зв’язування, англ.“most binding”). Це означає, що у будь-якому вираженні Python спочатку оцінить оператори та вирази, розташовані нижче в таблиці, а потім ті, що перераховані вище в таблиці.

Для повноти опису наведено наступну таблицю, взяту з Посібника мови Python (uk-flagанглійська: Python reference manual). Набагато краще використовувати дужки для відповідного групування операторів і операндів, щоб явно вказати порядок обчислення виразів. Це робить програму більш читабельною. Див. Зміна порядку оцінювання (uk-flagанглійська: Changing the Order of Evaluation) нижче для отримання додаткової інформації.

  • lambda : Лямбда-вираз (uk-flagанглійська: Lambda Expression)

  • if - else: Умовний вираз (uk-flagанглійська: Conditional expression)

  • or : Логічне АБО (uk-flagанглійська: Boolean OR)

  • and : Логічне І (uk-flagанглійська: Boolean AND)

  • not x : Логічне НЕ (uk-flagанглійська: Boolean NOT)

  • in, not in, is, is not, <, <=, >, >=, !=, == : Порівняння, включаючи тести на приналежність і тести на тотожність

  • | : Побітове АБО (uk-flagанглійська: Bitwise OR)

  • ^ : Побітове ВИКЛЮЧНО АБО (uk-flagанглійська: Bitwise XOR)

  • & : Побітове I (uk-flagанглійська: Bitwise AND)

  • <<, >> : Зміщеня (uk-flagанглійська: Shifts)

  • +, - : Додавання і віднімання(uk-flagанглійська: Addition and subtraction)

  • *, /, //, % : Множення, ділення, цілочисельне ділення та залишок від ділення (uk-flagанглійська: Multiplication, Division, Floor Division and Remainder)

  • +x, -x, ~x : Позитивне, негативне, побітове НЕ (uk-flagанглійська: Positive, Negative, bitwise NOT)

  • ** : Піднесення до степеня (uk-flagанглійська: Exponentiation)

  • x[index], x[index:index], x(arguments...), x.attribute : Звернення за індексом,зріз,виклик функції, посилання на атрибут (uk-flagанглійська: Subscription, slicing, call, attribute reference)

  • (expressions,..), [expressions,..], {key: value,..}, {expressions...} : Зв’язка або кортеж, список, словник, множина (uk-flagанглійська: Binding or tuple display, list display, dictionary display, set display)

Оператори, які ми ще не зустрічали, будуть пояснені в наступних розділах.

Оператори з однаковим пріоритетом містяться в одному рядку у наведеній вище таблиці. Наприклад, «+» і «-» мають однаковий пріоритет.

Зміна порядку обчислення#

uk-flagанглійська: Changing the Order Of Evaluation

Щоб зробити вирази більш зрозумілими, ми можемо використовувати круглі дужки.Наприклад, 2 + (3 * 4) легше зрозуміти, ніж 2 + 3 * 4, яке вимагає знання пріоритетів операторів. Як і в усьому іншому, дужки слід використовувати розумно (не перестарайтеся) і вони не повинні бути зайвими, як у (2 + (3 * 4)).

Є додаткова перевага використання круглих дужок - це допомагає нам змінити порядок обчислення. Наприклад, якщо ви хочете, щоб додавання обчислювалося перед множенням у виразі, ви можете написати щось на зразок (2 + 3) * 4.

Асоціативність#

Оператори зазвичай обробляються зліва направо. Це означає, що оператори з однаковим пріоритетом обчислюються зліва направо. Наприклад, “2 + 3 + 4” обчислюється як “(2 + 3) + 4”.

Вирази#

uk-flagанглійська: Expressions

код Python expression_ukr.py

довжина = 5
ширина = 2

площа = довжина * ширина
print('Площа дорівнює', площа)
print('Периметр дорівнює', 2 * (довжина + ширина))

Висновок:

$ python expression_ukr.py
Площа дорівнює 10
Периметр дорівнює 14

Як це працює

Довжина і ширина прямокутника зберігаються в однойменних змінних (довжина та ширина) відповідно. Ми використовуємо їх для обчислення площі та периметра прямокутника за допомогою виразів. Ми зберігаємо результат виразу довжина * ширина у змінній площа, а потім друкуємо його за допомогою функції print. У другому випадку ми безпосередньо використовуємо значення виразу 2 * (довжина + ширина) у функції друку.

Також зверніть увагу на те, як Python “гарно друкує” результат. Навіть незважаючи на те, що не вказано пробіл у кінці речення у лапках 'Площа дорівнює', Python розміщує його для нас, щоб ми отримали чистий гарний результат, і програма стала набагато читабельнішою таким чином (оскільки не потрібно турбуватися про пробіли в рядках, які ми використовуємо для виведення(друку)). Це приклад того, як Python полегшує життя програміста.

Резюме#

Ми побачили, як використовувати оператори, операнди та вирази - це основні будівельні блоки будь-якої програми. Далі ми побачимо, як використовувати їх у наших програмах за допомогою statements (операторів).

– Від перекладачa –

Розуміння двійкових цифр#

Двійкове число (uk-flagанглійська: binary number) - це число, виражене у двійковій системі числення, використовуючи лише два різні символи, як 0 і 1.

Щоб краще зрозуміти двійкову систему числення, давайте спочатку розглянемо більш популярну десяткову систему числення, uk-flagанглійська: decimal numeral system:

Вона містить 10 різних символів (0,1,2,3,4,5,6,7,8 і 9).

Щоб записати число більше 9, потрібно використати 2 або більше таких символів.

Наприклад, щоб записати число тридцять шість у десятковій системі, потрібно написати:

36

Тридцять шість — це двозначне число, тобто для його опису потрібні два символи.

Якщо читати обидва символи зліва направо, вони утворюють інструкцію обчислення:

36 (двозначне число)
розрахувати:
3 x 10 + 6 x 1 =
30 + 6 = 
36

Цікава частина цього полягає в тому, що лівий символ (3) має бути обчислений на 10, а правий символ (6) має бути обчислений на одиницю, а сума обох операцій представляє число.

Щоб записати число, більше 99, потрібні три цифри. Наприклад, щоб записати число дев’ятсот сорок два, потрібно написати:

942 (тризначне число)
читати зліва направо:
9 x 100 + 4 x 10 + 2 x 1 = 
900 + 40 + 2 = 
942

Оскільки число складається з трьох цифр, перший символ потрібно помножити на 100, другий на 10 і третій на 1.

Цю десяткову систему числення також називають системою з основою 10.

Коефіцієнти для множення символів на (1,10,100,…) можна записати у вигляді степенів основи 10:

100 =    1
101 =   10 
102 =  100
103 = 1000
і так далі...

Інструкцію з розрахунку числа 942 також можна записати так:

942:
9 x 102 + 4 x 101 + 2 x 100 =
9 x 100 + 4 x 10 + 2 x 1 =
900 + 40 + 2 = 
942

Двійкова система числення#

Двійкова система має основу не 10, а 2:

20 =   1
21 =   2
22 =   4
23 =   8
24 =  16
25 =  32
26 =  64
27 = 128
і так далі...

Однозначні числа в двійковій системі можуть відображати тільки числа 0 і 1:

щоб виразити число нуль, ви пишете:

0:
0 x 20 =
0 x 1 =
0

щоб виразити число один, ви пишете:

1:
1 x 20 =
1 x 1 =
1

і для будь-якого числа, більшого за 1, необхідно більше цифр.

Для числа два ви пишете 10:

10 (binary):
1 x 21 + 0 x 20=
1 x 2 + 0 x 1=
2 (decimal)

Для числа три ви пишете 11:

11 (binary):
1 x 21 + 1 x 20=
1 x 2 + 1 x 1=
2 + 1 =
3 (decimal)

А для числа чотири потрібні вже три цифри:

100 (у двійковій системі, чотири у десятковій системі)
1 x 22 + 0 x 21 + 0 x 20=
1 x 4 + 0 x 2 + 0 x 1 =
4 + 0 + 0 =
4

Двійкові числа проти десяткових чисел#

У цій таблиці порівнюються десяткова та двойкова системи числення

10-ва система

розрахунок

написання

2-ва система

розрахунок

0

0x100

нуль

0

0x20

1

1x100

один

1

1x20

2

2x100

два

10

1x21+0x20

3

3x100

три

11

1x21+1x20

4

4x100

чотири

100

1x22+0x21+0x20

5

5x100

п’ять

101

1x22+0x21+1x20

6

6x100

шість

110

1x22+1x21+0x20

7

7x100

сім

111

1x22+1x21+1x20

8

8x100

вісім

1000

1x23+0x22+0x21+0x20

9

9x100

дев’ять

1001

1x23+0x22+0x21+1x20

10

1x101+0x100

десять

1010

1x23+0x22+1x21+0x20

11

1x101+1x100

одинадцять

1011

1x23+0x22+1x21+1x20

12

1x101+2x100

дванадцять

1100

1x23+1x22+0x21+0x20

13

1x101+3x100

тринадцять

1101

1x23+1x22+0x21+1x20

14

1x101+4x100

чотирнадцять

1110

1x23+1x22+1x21+0x20

15

1x101+5x100

п’ятнадцять

1111

1x23+1x22+1x21+1x20

16

1x101+6x100

шістнадцять

10000

1x24+0x23+0x22+0x21+0x20

Як перетворити двійкову систему у десяткову#

Необхідно записати основу (2) у степені (цифр):

як перетворити число з основою 2 1001 на число з основою 10 (```9``):

число у двійковій системі:

1

0

0

1

степінь:

3

2

1

0

=

23

22

21

20

=

8

4

2

1

розрахунок:

8 +

0 +

0 +

1=

результат: 9

У Pyhton ви можете просто написати префікс 0b перед числом, щоб вказати, що ви використовуєте двійкову систему. Python миттєво перетворює число на десяткову систему:

>>>0b1001
9

Як перетворити десяткову систему у двійкову#

Вам потрібно записати основу (2) у степені (цифри). Потім ви починаєте справа наліво встановлювати піднесення до степеня з основою 2 у порядку зростання, до того моменту поки сума всіх встановлених бітів є меншою або дорівнює числу з основою 10.

Приклад:

як перетворити число з основою 10 (37) у число з основою 2 (100101):

степінь:

5

4

3

2

1

0

25

24

23

22

21

20

32

16

8

4

2

1

встановлений біт:

1

0

0

1

0

1

37 =

32+

0+

0+

4+

0+

1

двойкова система: 100101

У Python ви просто використовуєте вбудовану функцію bin(), щоб перетворити число з основою 10 у число з основою 2 (з префіксом 0b):

>>>bin(37)
'0b100101'

Оператори зсуву вліво на задану кількість біт#

uk-flagанглійська: left shift operation

Дивіться також статтю у Вікіпедії про Logical Shift

Операцію зсуву вліво можна виконати лише для двійкового числа (з основою 2). Простіше кажучи, усі числа переміщуються ліворуч, а крайні праві позиції заповнюються нулями. Знаком оператора є <<, і ви можете вказати, на скільки позицій ліворуч мають бути переміщені числа.

Приклад: виконайте операцію “зрушення вліво на 1” над двійковим числом 1001 (дев’ять за основою 10). Результат: 10010 (вісімнадцять за основою 10).

код Python left_shift_ukr.py

print("У двійковій системі:")
print("0b1001<<1")
print("=")
print(bin(0b1001<<1))
print()
print("У десятковій системі:")
print(0b1001, "<<1 =", 0b1001<<1)

Висновок:

У двійковій системі:
 0b1001<<1
=
0b10010

У десятковій системі:
9 <<1 = 18

Зображення нижче зі статті у Вікіпедії:

MSB = старший біт, LSB = молодший значущий біт

Зауважте, що біт, якби старший біт (MSB, число 7) був би 1, результуюче число було б більшим, як у прикладі вище.

left shift

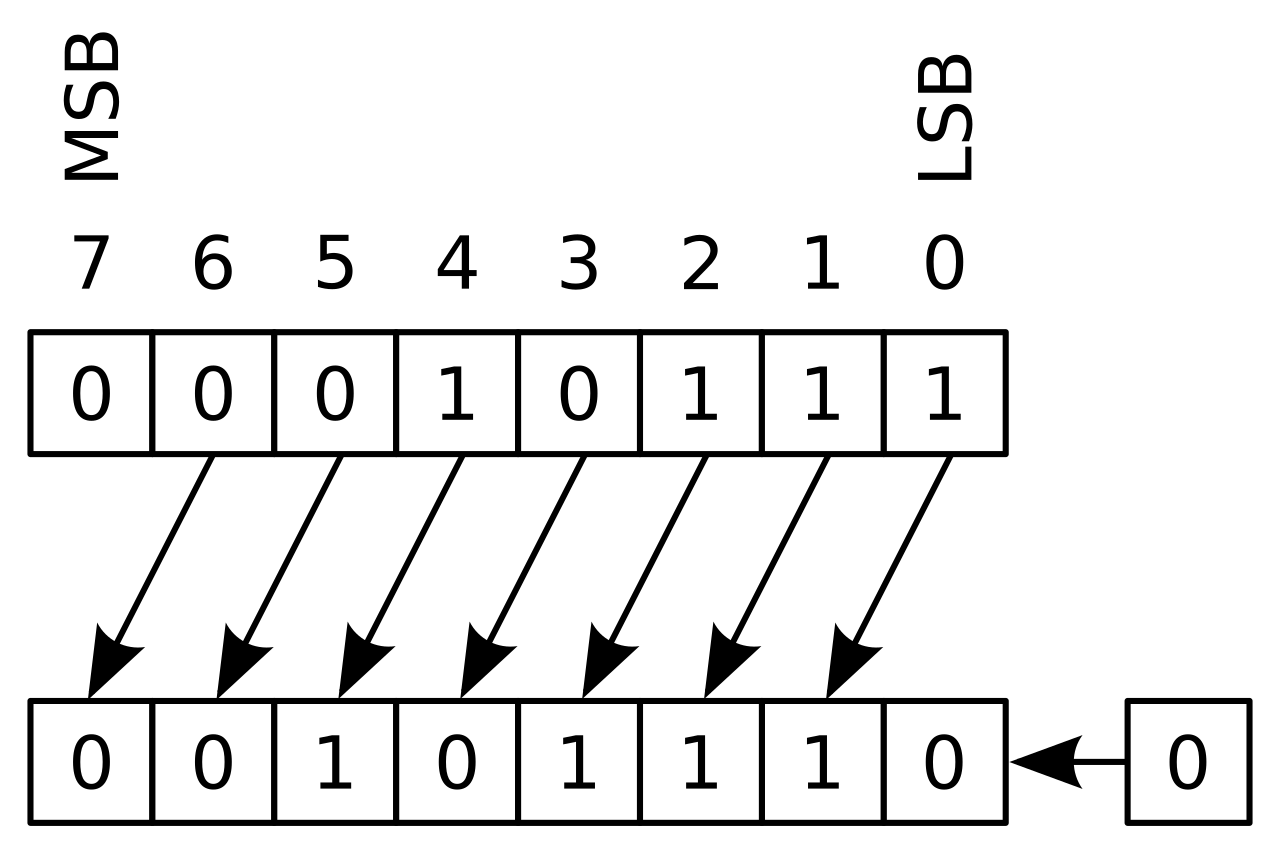
_images/Rotate_left_logically.svg.png

Опис зображення: 0001 0111 (десяткове число 23) логічно зсувається на один біт вліво, результат 0010 1110 (десяткове число 46).#

Image rights: By en:User:Cburnett - This W3C-unspecified vector image was created with Inkscape ., CC BY-SA 3.0, Link

Оператори зсуву вправо на задану кількість біт#

uk-flagанглійська: right shift operation

Дивіться також статтю у Вікіпедії про Logical Shift

Операція зсуву вправо працює трохи подібно до операції зсуву вліво: усі числа переміщуються праворуч, крайні ліві позиції заповнюються нулями, а числа, які були в крайній правій позиції, просто видаляються.

Знаком оператора є >>, і ви можете вказати, на скільки позицій праворуч слід перемістити кожне число.

Приклад: виконайте операцію «зсув праворуч на 1» над двійковим числом 1001 (дев’ять за основою 10). Результатом є 0100 і зазвичай записується без нуля на початку як 100 (чотири за основою 10).

код Python right_shift_ukr.py

print("У двійковій системі:")
print("0b1001>>1")
print("=")
print(" "+bin(0b1001>>1))
print()
print("У десятковій системі:")
print(0b1001, ">>1 =", 0b1001>>1)

Висновок:

У двійковій системі:
0b1001>>1
=
 0b100

У десятковій системі:
9 >>1 = 4

Зображення нижче зі статті у Вікіпедії:

MSB = старший біт, LSB = молодший значущий біт

Зауважте, що на зображенні нижче молодший значущий біт (LSB) знищується

right shift

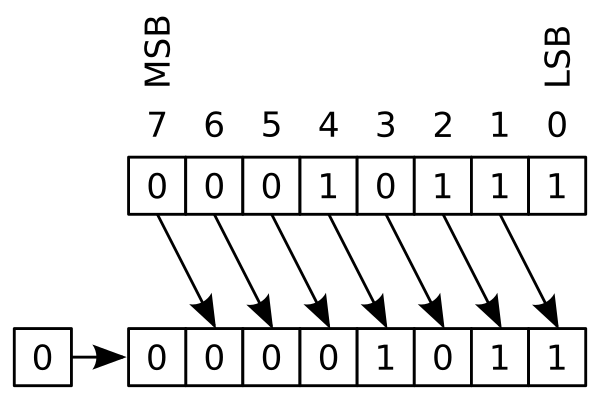
_images/Rotate_right_logically.svg.png

Опис зображення: 0001 0111 (десяткове число 23) логічно зсувається на один біт вправо,результат буде: 0000 1011 (десяткове число 11)#

Image rights: By en:User:Cburnett - This W3C-unspecified vector image was created with Inkscape ., CC BY-SA 3.0, Link

Логічні оператори python#

uk-flagанглійська: boolean operators

значення A

значення B

результат для AND

результат для OR

True

True

True

True

True

False

False

True

False

True

False

True

False

False

False

False

Логічне НЕ#

uk-flagанглійська: NOT

Оператор NOT дає значення інвертування: True стає False, а False стає True.

операція

результат

not True

False

not False

True

Логічне І#

uk-flagанглійська: AND

Оператор AND повинен бути розміщений між двома логічними значеннями. Результатом буде True, якщо обидва логічні значення True, інакше результат буде False

значення A

AND

значення B

результат

True

AND

True

= True

True

AND

False

=False

False

AND

True

=False

False

AND

False

=False

Логічне АБО#

uk-flagанглійська: OR

Оператор АБО має бути розміщено між двома логічними значеннями. Результат є True, якщо одне або обидва значення є True. Результатом буде False, якщо обидва значення є False.

значення A

OR

значення B

результат

True

OR

True

= True

True

OR

False

=True

False

OR

True

=True

False

OR

False

=False

Логічні операції з двійковими цифрами#

uk-flagанглійська: boolean operations with binary digits

Логічні операції (and, or, xor, not) можуть бути застосовані не лише до логічних значень (True і False), а й безпосередньо до бітів (де 1 означає True, а 0 означає False).

У Python є логічні команди not or and для логічних значень, але є також спеціальний набір команд для двійкових цифр:

~  Побітове НЕ (for bitwise inversion)
|  Побітове АБО (for bitwise OR)
&  Побітове І (for bitwise AND)
^  Побітове виключне АБО (for bitwise XOR)

Побітове НЕ#

uk-flagанглійська: bitwise inversion

~ (bit-wise invert) - Побітова операція НЕ для числа x відповідає -(x+1). Значення: до числа додається 0b01 і змінюється знак.

код Python bitwise_inversion_ukr.py

print("Приклад 1:")
print("Припустимо x становить 1001")
print("Побітове НЕ те саме, що -(x+1)")
print("Обчислювання x+1 наступне : 1001 + 0001")
print("Кінцевий результат є -(1001 + 0001)")
print("~0b1001 = ")
print(bin(~0b1001))
print("=-(x+1)=-(0b1001 + 0b0001) = -0b1010")
print("Приклад 2:")
print("~-0b1111 = ")
print("  "+bin(~-0b1111))
print("=-(x+1)=-(-0b1111+0b0001)=-0b1110")

Висновок:

Приклад 1:
Припустимо x становить 1001
Побітове НЕ те саме, що -(x+1)
Обчислювання x+1 наступне : 1001 + 0001
Кінцевий результат є -(1001 + 0001)
~0b1001 = 
-0b1010
=-(x+1)=-(0b1001 + 0b0001) = -0b1010
Приклад 2:
~-0b1111 = 
  0b1110
=-(x+1)=-(-0b1111+0b0001)=-0b1110

Побітове І#

uk-flagанглійська: bitwise and

  • &(побітове І, англ.“bit-wise AND”)

    • Побітова операція І над числами: якщо обидва біти дорівнюють 1, то результат дорівнює 1. В іншому випадку це 0.

Приклад A

Приклад B

Приклад C

0b1100

0b1111

0b1011

&

&

&

0b0101

0b0000

0b0001

=

=

=

0b0100

0b0000

0b0001

Побітне АБО#

uk-flagанглійська: bitwise or, inclusive OR

  • | (bit-wise OR)

    • Побітова операція АБО над числами: якщо обидва біти дорівнюють 0, результат 0. В іншому випадку це 1.

Приклад A

Приклад B

Приклад C

0b1100

0b1111

0b1011

|

|

|

0b0101

0b0000

0b0001

=

=

=

0b1101

0b1111

0b1011

Побітне ВИКЛЮЧНО АБО#

uk-flagанглійська: bitwise xor, exclusive OR

  • ^ (bit-wise XOR)

    • Побітова операція виключне АБО над числами: якщо обидва біти (1 або 0) однакові, результат дорівнює 0. В іншому випадку це 1.

Приклад A

Приклад B

Приклад C

0b1100

0b1111

0b1011

^

^

^

0b0101

0b0000

0b0001

=

=

=

0b1001

0b1111

0b1010
Зміст